Wait, I’m Actually Using Math in Real Life? Two Formulas Essential to Financial Intelligence

Okay, so we all remember nodding off to sleep during an algebra lesson and, after being rudely awakened by the teacher, murmuring something along the lines of “It’s not like we’re going to use this stuff anyway.” Turns out, some of it, we will.

That’s not to say that the entire school system is absolved from blame of teaching thousands of concepts that will not and never will be used in any context other than the classroom—no, the school system should be held accountable for regularly prioritizing theoretical concepts over real-life skills, but that is a discussion for another day.

For today, the topic revolves around revisiting some of those principles from algebra to make sense of two formulas that are essential for anyone seeking financial intelligence. And, really, that should be all of us—financial intelligence leads to financial freedom and financial freedom leads to, well, happiness. I’m not suggesting that financial freedom is the sole requirement for happiness, but it certainly doesn’t hurt.

Before I introduce these formulas, know that I am fully aware that the internet is loaded with compound interest calculators to do this work for you and, although most of them are linked to a series of ads for mortgages and lines of credit, they make the number crunching fairly easy. Here’s the thing—take ownership of your money. When you understand how the calculations work, it empowers you to take charge of your finances.

We’re going to take a look at two formulas as an introduction to the time value of money that will make an intelligent investor out of all us if properly understood. The first is the formula to determine the future value of a lump sum of cash.

FV=PV(1+r)ⁿ

Here the future value (FV) is calculated by taking the present value (PV) and multiplying it by the sum of the interest rate (written in decimal form) and the number 1 which is then taken to the power of the number of periods (in years).

In other words, let’s say that you have $1,000 to invest. That is your present value (PV). You can assume, based on averages with investments in the stock market (another subject that will be discussed at a later point), a 10% interest rate (r), and you want to invest it for 10 years (n). The formula now looks like this:

FV=1,000(1+.10)10

In this calculation, your future value (FV) turns out to be $2,593.74. Now consider that for just a moment: over the course of 10 years, earning a steady 10% a year, that $1,000 is now worth over $2,500. One important thing to keep in mind is that this calculation assumes there will be no additional contributions—just the one lump sum. Even without contributions, that money quickly begins to make money and then the money it makes, makes money.

The fallacy most people bring to the equation of interest is forgetting that interest compounds. One could easily assume that $1,000 invested at 10% makes $100 a year, and that after ten years, one would have $2,000. That extra $593 on top of the $2,000 is the beauty of compound interest—and it just gets higher and higher. Consider the same formula but with 20 years instead of ten, so it looks like this:

FV=1,000(1+.10)20

Now you’ve got a future value of $6,727.50. And that’s starting with the same $1,000. By the logic presented earlier, one would assume that, earning 10% a year, year after year, you should have $3,000 at the end of twenty years, but the compounding effect of the interest inherent in this formula demonstrates clearly what Einstein said about compound interest being the eighth wonder of the world—“he who understands it, earns it . . . he who doesn’t, pays it.”

For our second formula, we are going to work backward—determining what we need as a present value (PV) to reach a set future value (FV). Suppose we want to retire with two million dollars. We know that we want to retire by age 65, so we want to find out just how much we would need now to meet that goal by age 65. Again, this assumes we are not doing regular contributions but are just looking at a lump sum.

Here’s the formula in reverse:

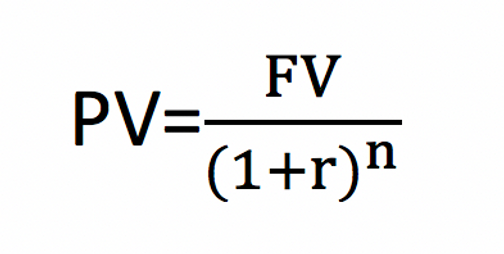
We want to determine what our present value (PV) needs to be in order to reach a desired future value (FV). For our intent, we are going to consider it from the perspective of retirement, wanting $2,000,000 in the bank. Again, we are assuming a 10% interest rate and the number of years depends on how long we have to save. If we are, say, 35 years old, we can assume we have 30 years before retirement. Our formula would look like this:

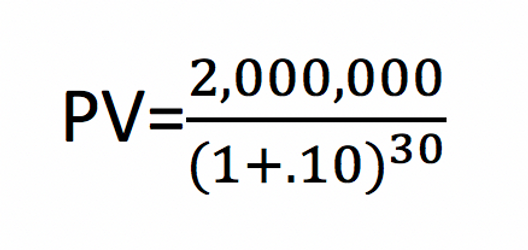
In this calculation, the present value (PV) turns out to be $114,617. Seriously—just $114,617. Over a period of 30 years, with no additional contributions, that amount would turn into $2,000,000 due to, you guessed it, the beauty of compound interest.

This is the kind of math I can get behind—the dream of retiring a millionaire is within everyone’s grasp when you consider that, over time, money makes money which makes money. The truth is, these formulas are fun—there’s nothing like sitting around projecting timelines into the future and considering what your present lump sum might turn into in, say, 10 or 20 years. It may even be a deterrent to spending—before you drop $800 on a new set of golf clubs, just remember that, in five years, that could be worth $1,288.

Just some food for thought—and a reminder to occasionally stay awake in math class.